Compound Interest

Compound interest (or compounding interest) is the interest on a loan or deposit calculated based on both the initial principal and the accumulated interest from previous periods. Thought to have originated in 17th century Italy, compound interest can be thought of as "interest on interest," and will make a sum grow at a faster rate than simple interest, which is calculated only on the principal amount.

KEY TAKEAWAYS

Compound interest (or compounding interest) is interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods on a deposit or loan.

• Compound interest is calculated by multiplying the initial principal amount by one plus the annual interest rate raised to the number of compound periods minus one.

• Interest can be compounded on any given frequency schedule, from continuous to daily to annually.

• When calculating compound interest, the number of compounding periods makes a significant difference.

The rate at which compound interest accrues depends on the frequency of compounding, such that the higher the number of compounding periods, the greater the compound interest. Thus, the amount of compound interest accrued on $100 compounded at 10% annually will be lower than that on $100 compounded at 5% semi-annually over the same time period. Since the interest-on-interest effect can generate increasingly positive returns based on the initial principal amount, it has sometimes been referred to as the "miracle of compound interest."

Calculating- Compound interest is calculated by multiplying the initial principal amount by one plus the annual interest rate raised to the number of compound periods minus one. The total initial amount of the loan is then subtracted from the resulting value.

Compound Interest = Total amount of Principal and Interest in future (or Future Value) less Principal amount at present (or Present Value)

= [P (1 + i)n] – P

= P [(1 + i)n – 1]

(Where P = Principal, i = nominal annual interest rate in percentage terms, and n = number of compounding periods.)

Take a three-year loan of $10,000 at an interest rate of 5% that compounds annually. What would be the amount of interest? In this case, it would be: $10,000 [(1 + 0.05)3 – 1] = $10,000 [1.157625 – 1] = $1,576.25.

Growth of Compound Interest 

Using the above example, since compound interest also takes into consideration accumulated interest in previous periods, the interest amount is not the same for all three years, as it would be with simple interest. While the total interest payable over the three-year period of this loan is $1,576.25, the interest payable at the end of each year is shown in the table below.

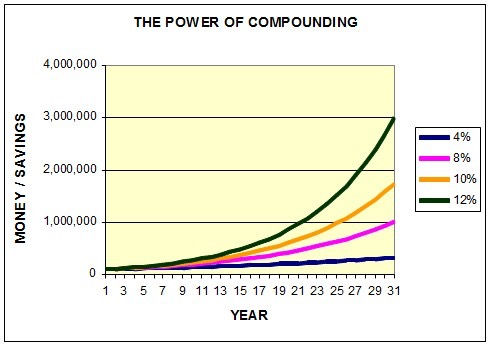
Compound interest shows how much money a person can develop over time at an exponential rate. Each year your money is invested, it grows in an exponential direction that can have a person net hundreds of thousands or even millions of dollars when they retire. By taking advantage of compound interest with your money, your portfolios can increase at a much higher rate.